Se tem uma coisa de que gosto muito na costura e admiro aqueles que sabem e ensinam com honestidade é o saber calcular e fazer moldes. Tanto na costura de roupas quanto na de acessórios.
Não acho, como alguns, que a modelagem é essencial na costura criativa e sem ela nada sai bem feito. Errado!
Minha experiência de 17 anos na costura artesanal me mostra que não há uma fórmula rígida para se fazer costura artesanal bonita e bem feita.
Veja que eu gosto de estudar modelagem, sei alguma coisa sobre, mas não considero uma condição fundamental saber fazer um molde de necessaire para se poder fazê-la bem feita.
E tem os defensores ferrenhos dos moldes que dizem ensinar como fazer, mas, na verdade, não é bem assim. Modelagem é geometria e matemática, é raciocínio lógico e nem todos estão assim tão dispostos a ensinar como raciocinar fórmulas simples.
Quer um exemplo de como é possível chegar a um resultado exato através de raciocínio matemático simples?
Vamos começar por aqui, então, os bolsos externos com foles ao redor: como fazer e como aplicá-los
Como calcular as medidas exatas de um retângulo com cantos arredondados para fixar-lhe fole e anel de zíper ?
Suponha que eu tenha um quadrado de 12 cm x 12 cm:

E que eu queira arredondar suavemente suas bordas: escolho um arredondamento de 2,5 cm. Para tanto eu preciso de uma circunferência de 5,0 cm de diâmetro (abro o compasso com 5,0 cm de abertura e traço um círculo)
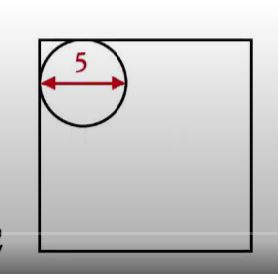
Ao encostar o círculo ao canto do quadrado (suponha que seja um círculo de papelão que você traçou, recortou e colocou como molde para o traçado), ao encostar ali eu tenho o traçado perfeito de 2,5 cm, o que chamamos de raio em Matemática. 2,5 cm de raio. Arredondo, desse modo, os quatro cantos com 2,5 cm (de raio). O raio é sempre a metade da medida do diâmetro.

E se quiser testar as medidas, é só traçar um quadrado de 2,5 cm x 2,5 cm do modo como vê na imagem.
Minha figura ganhou cantos arredondados e, portanto, medir a área dessa figura, ou seja, saber a medida exata desse contorno já não é mais um cálculo tão simples como era se fosse o quadrado de 12 cm x 12 cm.
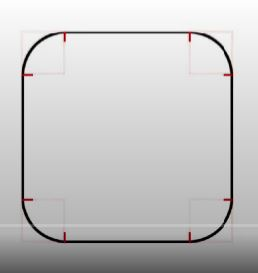
Se eu possuia um quadrado com 12 cms de lado, agora essas linhas retas de 12 cm diminuiram de tamanho pra tornarem as bordas arredondadas. Imagine você pegando um arame flexível de 12 centímetros e curvando com as mãos as extremidades. O que era reta, virou curva.
Aqui nós vamos começar a calcular, portanto, a medida de todo esse contorno através de raciocínio matemático, sem a interferência da fita métrica, por enquanto, que tal? 😉
Vamos saber quantos centímetros medem cada um dos lados retos que antes mediam 12 cm. Até aí me parece fácil: Da reta de 12 cm eu diminuo 2,5 cm de cada extremidade, que dará 5,0 cm, ou seja, 12 cm – 5 cm = 7,0 cm.
Cada segmento reto, sem curva, mede 7,0 cm. E você pode usar sua régua ou fita métrica para conferir isso:

Agora, me diga uma coisa: eu preciso cortar um “anel” de tecido para costurar no contorno desse quadrado com cantos arredondados. Como faço para saber a medida exata desse contorno para fazer o corte do meu tecido?
Aí, meus caros leitores, entra uma fórmula matemática e mágica!!!
Você vai somar a medida de todos os lados retos, ou seja, 7+7+7+7
Lembra da circunferência de 5 diâmetros que modificou os quatro lados daquele quadrado?
Então, agora você vai pegar o diâmetro desse círculo e multiplicar por um valor que é fixo e não muda, pois faz parte da nossa fórmula. Na escola eu aprendi que esse número é o valor de Pi, um símbolo que não tenho aqui no teclado, mas que pouco importa porque teremos sempre esse mesmo raciocínio, ou seja:
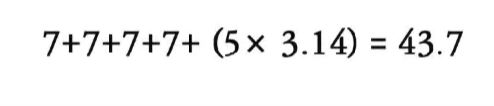
Então, minha gente, o comprimento do tecido que preciso para costurar ao redor dessa elipse, que no começo era um quadrado, é de 43.7 centímetros. Sem nenhuma margem de costura.
Ao fazer o molde, claro, você vai adicionar a margem de costura nas figuras onde houver costuras. O que importa aqui, enfim, é demonstrar o raciocínio necessário para se chegar às medidas e, veja, é simples, resume-se nessa fórmula acima e com uma calculadora você chega ao resultado sem grande esforço e sem depender de um molde pronto ou de uma explicação pela metade como tantas que tem por aí.
É claro que hoje é fácil você abrir um programa gráfico como o Corel, por exemplo, e ele fará tudo automaticamente para você.
Ou mesmo aplicativos para traçar moldes. Ou até a Inteligência Artificial.
Mas eu ainda sou do tempo em que a liberdade residia no conhecimento. Se você gostou dessa demonstração, use a fórmula, teste nos seus moldes usando apenas uma calculadora. O valor de 3.14 é fixo, é o multiplicador da circunferência que você usou.
Não importa a medida de seu diâmetro, esse multiplicador de 3.14 não muda.
Vamos supor que você queira fazer uma bolsinha crossbody retangular onde o retângulo inicial tem 25 cm x 18 cm e vai receber arredondamento nas extremidades de 3,0 centímetros.
1- Pergunta-se : Qual o perímetro(soma dos 4 lados) desse retângulo (sem os arredondamentos) ?
2 – Pergunta-se : Qual o diâmetro dessa circunferência de 3 cm de raio?
3 – Depois de aplicadas as curvas nas 4 extremidades, qual o tamanho das retas dos 4 lados?
4 – Aplicada a fórmula que você aprendeu na explicação anterior, diga qual a medida do perímetro dessa figura agora retangular com cantos arredondados? O resultado dessa fórmula é o tamanho exato do material que você precisará cortar para costurar ao redor da figura. Sem costuras, claro. Nada mal, hein?
Na verdade, ao utilizar essa fórmula é como se você transformasse toda essa figura numa reta e calculasse seu comprimento.
Sabe aquele arame que você curvou com as mãos? É como endireitá-lo, deixando-o reto para medir seu comprimento. Não é lindo quando podemos raciocinar sobre? Tudo isso está aqui em nossa costura artesanal!!!
Qualquer dúvida ou caso queira conferir o resultado, mande e-mail para artecomtecidos@artecomtecidos.com.br
Bolsos externos: show de explicação!

Depois de toda essa explicação matemática, você não vai ter a menor dificuldadde em calcular os foles desses bolsinhos externos. Concorda?
Vai saber construir e aplicar com facilidade, usando OUT STITCH = COSTURA EXTERNA; INSIDE STITCH = COSTURA INTERNA; BACK OPEN = ABERTO ATRÁS.
Neste vídeo você aprende tudinho, desde o modo de calcular o tamanho dos foles do bolso até o modo de aplicá-los na mochila, na bolsa ou na necessaire. Bora aprender? É neste link o canal do vídeo.
